Cryptanalysis of the Algorand Subset-Sum Hash Function (UPDATED 25th June 2022)

Dmitry Khovratovich | June 25, 2022

1. Introduction

Algorand has proposed a compression function which is lattice-ZKP friendly and which they plan to use inside the Merkle-Damgard framework.

The public constants of the function are matrix $A\in Z_q^{n\times m}$ where $q=2^{64}, n=8, m=1024$. Let us denote the columns of $A$ by $A_i$, $0\leq i <m$. Matrix entries should be pseudorandomly generated.

The compression function $f_A$ processes the $m$-bit input $\mathbf{x} = (x_0,x_1,\ldots,x_{m-1})$ as follows:

with the input interpreted as a $n\log q = 512$-bit value.

The authors claim one-wayness of the compression function, though not mentioning any concrete security level.

2. Generalized birthday problem

The generalized birthday problem was first formulated by Wagner as follows:

Given lists $L_1,L_2,\ldots,L_{2^k}$ of binary $n$-bit strings find $l_i\in L_i$ such that

For $k=1$ it is the standard birthday problem and a solution can be found in $2^{n/2}$ time (for that big lists). It is less obvious that for $k>1$ one can do better than $2^{n/2}$, concretely in $2^{\frac{n}{k+1}}$ time. The idea can be illustrated for $k=2$:

• Find $2^{n/3}$ \emph{partial collisions} between $L_1$ and $L_2$ i.e. strings that collide in the first $n/3$ bits. This can be done in $2^{n/3}$ time by taking $2^{n/3}$ elements from both lists and sorting them by the first bits. Put collisions and their components into new list $X = \{(l_1\oplus l_2,l_1,l_2)\}$
• Repeat the same for lists $L_3$ and $L_4$ and obtain list $Y$.
• Find tuples $(x,l_1,l_2)\in X$ and $(y,l_3,l_4)\in Y$ such that $x=y$. This is feasible since both $x$ and $y$ are zero in the first $n/3$ bits so we need only $2^{n/3}$ tuples in both lists to find a collision on the remaining $2n/3$ bits.

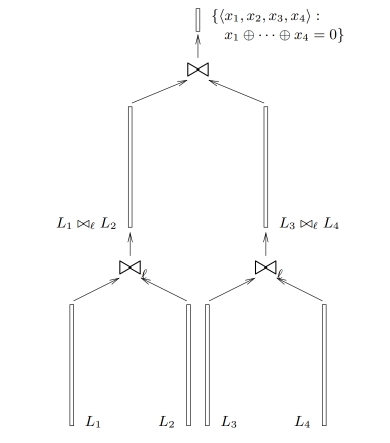
The same approach works for bigger $k$. Note though that there is no such algorithms for 3 lists $L_1,L_2,L_3$ and the best attack is still $O(2^{n/2})$.

Finally remark that the process is memory-heavy for $k>1$. This fact is used in the memory-hard proof-of-work Equihash, used in Zcash.

3. Attack on the Algorand hash

The compression function described in Section 1 is vulnerable to a modification of the generalized birthday attack. Let us find a collision:

We do as follows:

• Split the $\mathbf{x},\mathbf{y}$ into 16 64-bit chunks $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_{16},\mathbf{y}_1,\mathbf{y}_2,\ldots,\mathbf{y}_{16}$.
• Interpret the output $f_A(\mathbf{x})$ as a 6-tuple $(a_1,a_2,a_3,a_4,a_5,a_6)$ where $a_1$ is 32-bit and all other $a_i$ are 96-bit.
• For all $2^{64+64}$ pairs $(\mathbf{x}_{i},\mathbf{y}_{i}), i<8$, find $2^{64+64-32}=2^{96}$ collisions for $f_A$ in $a_1$, i.e. solutions for

spending $2^{96}$ time and space for each $i$ using list sorting for birthday paradox. Store all solutions in lists $L_i$.

• For each $j<8$ find partial collisions between $L_{2j+1}$ and $L_{2j+2}$ in $a_2$:

Note that since both $z$ and $z'$ are 0 in $a_1$ they sum to 0 in it. The number of partial collisions between $L_{2j+1}$ and $L_{2j+2}$ is $2^{96+96-96}=2^{96}$. Store the results in 8 lists $L_k$.

• We now find $2^{96}$ partial collisions between pairs of lists in $a_3$ and obtain 4 lists. Then proceed the same way with $a_4$ and get two lists.
• Find a single collision between the two lists in $a_5$ and $a_6$ at cost $2^{96}$. It yields

i.e. a collision.

Overall the collision attack costs $2^{98}$ time (it is not necessary to work on all the lists simultaneously) and thus the overall security of the subset sum hash is at most 98 bits in the time cost model.

UPDATE (25 June 2022)

4. Bug in Section 3 and its fix

The Algorand team has kindly reported us a flaw in Section 3. Concretely, if one merges $f_A(\mathbf{x}_i)$ and $\mathbf{y}_i$ in the first step of the attack than due to the linearity of $f_A$ the number of possible pairs is $3^{64}$ rather than $4^{64}$, which makes the search for $2^{96}$ partial collisions more expensive.

The simple fix to this flaw is to merge instead $f_A(\mathbf{x}_1)$ with $f_A(\mathbf{x}_2)$, then $f_A(\mathbf{x}_3)$ with $f_A(\mathbf{x}_4)$, so that the inputs activate different scalars in $A$. When repeating for $f_A(\mathbf{y}_i)$, one should target different collision bits to avoid having $\mathbf{x}=\mathbf{y}$. The rest of the attack remains the same with the same complexity estimate.

5. Algorand internal analysis

In response to our original post, the Algorand team has published an internal analysis. The report investigates the complexity of the Wagner attack implemented on a quantum computer. For collision search the report estimates the quantum attack complexity as $2^{108}$ time and $2^{40}$ memory. The same document also gives the complexity of the classical Wagner attack as $2^{107}$ time and $2^{85}$ memory, which is a variation (another point on the time-area tradeoff curve) of our attack in Section 3, assuming our bugfix above.

Acknowledgements

We thank Chris Peikert for fruitful discussions that has led to the attack refinements.